
index structure
file에 제공되는 index는 보조 접근 구조이다
주어진 검색조건에 대응해 record를 검색할때 속도를 높여주기위한 목적으로 사용된다
기존에 저장되어 있는 물리적인 위치와 상관없이 대체방안을 제공하는 목적
indexing field에 대해 record를 효율적으로 검색하는 방법 제공

-single level index(정렬용도)
primary, secondary, and clustering
ISAM : 이 방법을 사용하는 file의 명칭
-multilevel indexes
btree 나 b+tree

Primary index
record가 정렬된 field에 대한 index
Clustering index
같은 방법으로 record가 정렬된 fiedl에 대해 index가 구성되는데, 그 field가 key가 아닌 것
같은 값을 같는 record가 여러개인 경우가 있다
file은 primary index , clustering index 둘중 한가지만 가질 수 있다.
Secondary index
-정렬되지 않은 field에 대한 인덱스
-Primary access method의 추가적인 보조기능 제공

Primary indexes
두 개의 field를 갖는 fixed length의 record형태의 file
index = <K,P> 키값, 그 키값이 저장되어 있는 주소
K : main file을 정렬하는 key field
P : disk block에 대한 포인터
한 index entry는 각각 데이터 블럭당 하나씩 존재한다
각각의 대표하는 하나의 record는 anchor record or block anchor라고 한다


모든 record에 대한 entry가 없기 때문에 sparse index라고 한다
모든 record데 대해 entry가 존재하는 경우 dense index라고 한다
Primary index = sparse index
secondary index =dense index






bfr=273 , 한 block에는 273개의 entry가 존재한다, block pointer는 7,500/273=28개가 필요하다
binary search의 경우 5idx block accesses + 1 data block access
index file의 크기가 작으면 MM에 위치시켜 한 블럭만으로 바로 찾아가는 방법이 가능하다

문제점
삽입,삭제등의 갱신이 부담스럽다
record를 삽입하기 위해서는
새로운 record를 위한 공간을 위해 record를 전부 움직여야하고, anchor record가 바뀌니 index file도 같이 바꿔주어야 한다
문제를 줄이기 위한 수단
-overflow file 사용
-linked list를 사용하여 찾아갈 수 있게 한다
record가 삭제되는 경우 delete marker 이용

Clustering index
정렬키가 nonkey field - clustering field
Ordering field가 특별한 값을 같는경우 primary index,그렇지 않으면 clustring index




Secondary Indexes
-특정 record 검색시 PK로만 하진 않는다, 검색을 빠르게 해주기 위해 다른 field에 대해 index를 만드는데 이것을 Scondary index라고 한다.
-dbms는 자동으로 primary index를 만들어준다
-block이 아닌 record당 하나의 entry가 생기기 때문에 dense index를 갖는다
-secondary index가 존재 하지 않으면 linear search를 해야하기 때문에, 이런 기능은 매우 효율적인 검색 기능을 제공해 준다


Secondary index의 key가 unique한 값을 갖는데 Nonkey Field인 경우
해당 키값 하나에 대해 여러가지 record가 발생
나올때마다 index entry를 중복시켜주는 방법
가변길이 entry를 이용하는 방법 (좋은 방법이 아니다)
level을 증가시킨 고정길이 entry를 이용 , P는 data 에 대한 pointer가 아닌 pointer들의 집합block에 대한 pointer
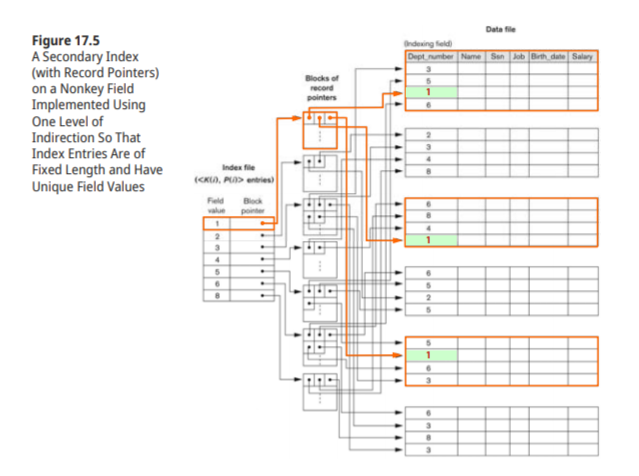

example 3
Secondary key-a nonrodering key field(대체 키)에 대한 record 검색
secondary index가 없을때와 , 있을때의 예
index entries가 record개수 전체인것에 유의해야 한다


Multilevel indexes
fan out : binary search같은 탐색의 branch 수
bfri = bfri개수만큼의 fan-out을 가진다=fo
bfri를 이용해 tree의 차수를 가지면 검색이 매우 빨라진다
탐색시간은 log2b = logfo(b)로 변경







B-trees
tree가 너무 한쪽으로 치우치면 트리의 장점을 전혀 받을 수 없다.
그렇기 때문에 balance를 유지하는것이 중요하고 이런 조건을 갖는것을 B-tree라고 한다 (B: balance)
임의의 삽입,삭제의 경우에도 tree의 balance를 맞춰준다
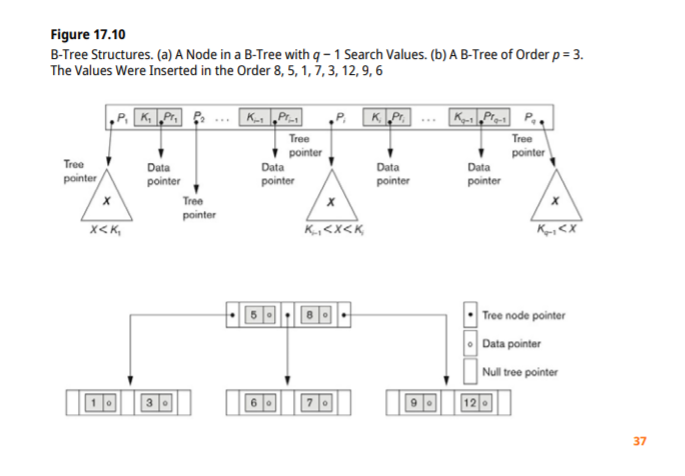










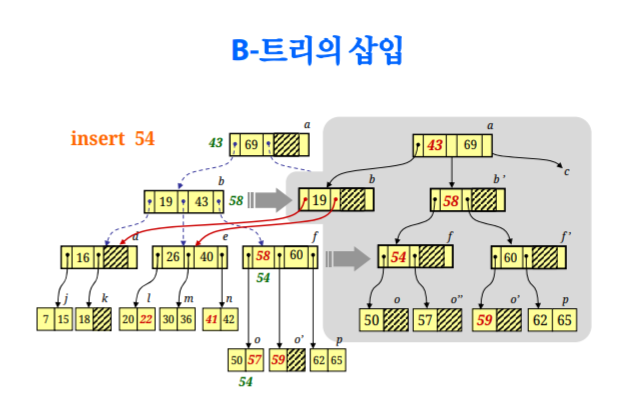








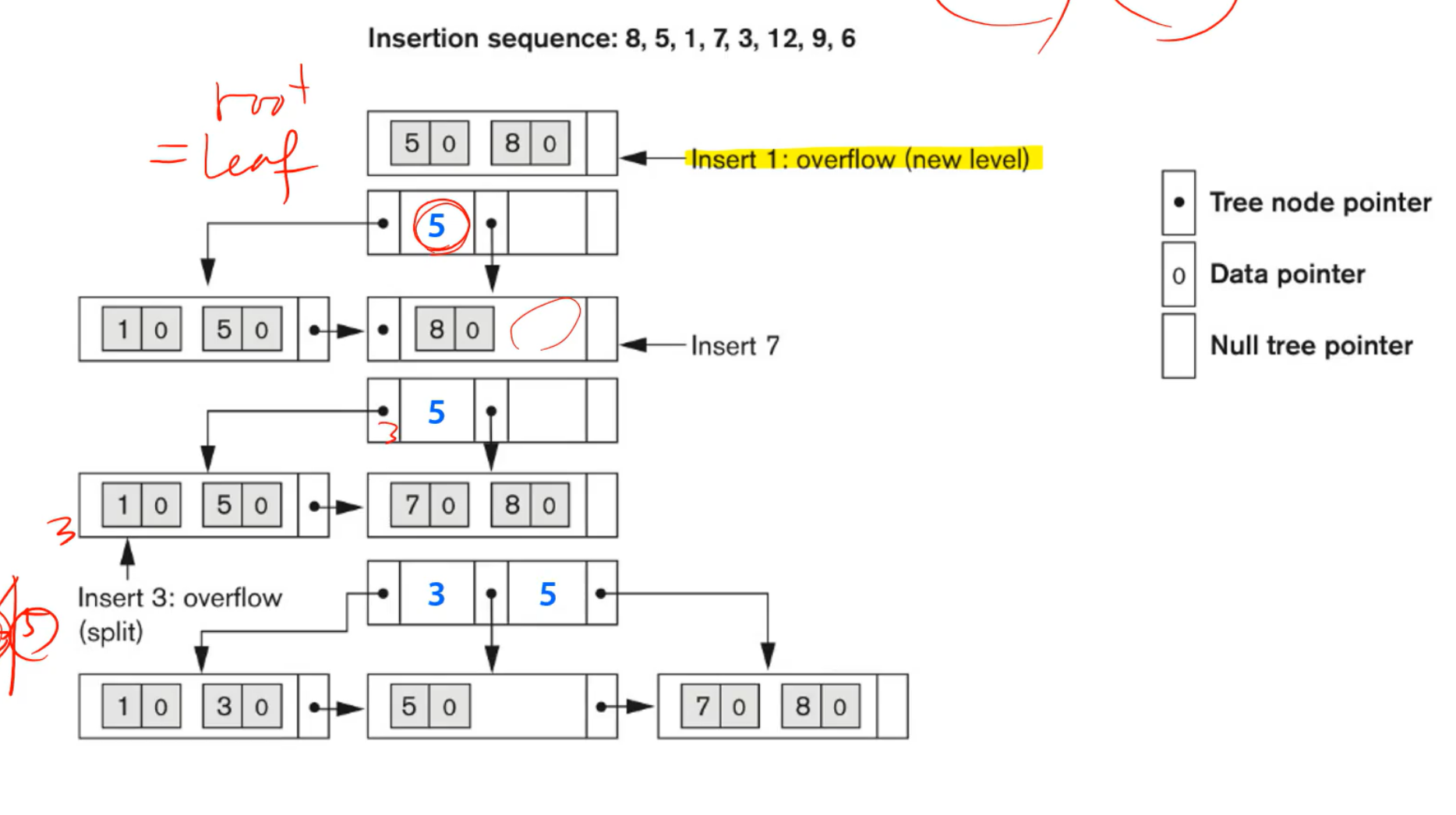
B+ TREE
BTREE의 변형으로서 data pointer가 leaf node에만 저장이 된다.
-중간 노드에는 data pointer가 없고 분기값만 저장되어 있다
-모든 data들은 leaf node에 반드시 entry가 있으며, leaf node를 가야 data를 판단할 수 있다.
-leaf node의 단말 node들은 순차탐색을 위해 자기들끼리 연결되어 있다
-linked list를 따라가면 순차 탐색이 가능하도록 구성되어 있다.



Example 6
V=9, B=512,Pr=7,P=6 공식을 이용해 p를 구하면 p=34이며, 아까의 Btree 보다 fan out이 상대적으로 커졌다는것을 알 수 있다.
data pointer가 존재하지 않아서 leaf 까지 가야 검색이 가능하다.


Example 7
p=34 일때, 데이터가 69프로 찬다고 가정할 때.
각 중간노드는, 23pointers를 가지고, key값은 22개
left node는, 21data pointers
entry,pointer 수를 보면 기존 Btree보다 level당 fanout이 훨씬 커지기 때문에 더 많은 양을 저장할 수 있다.



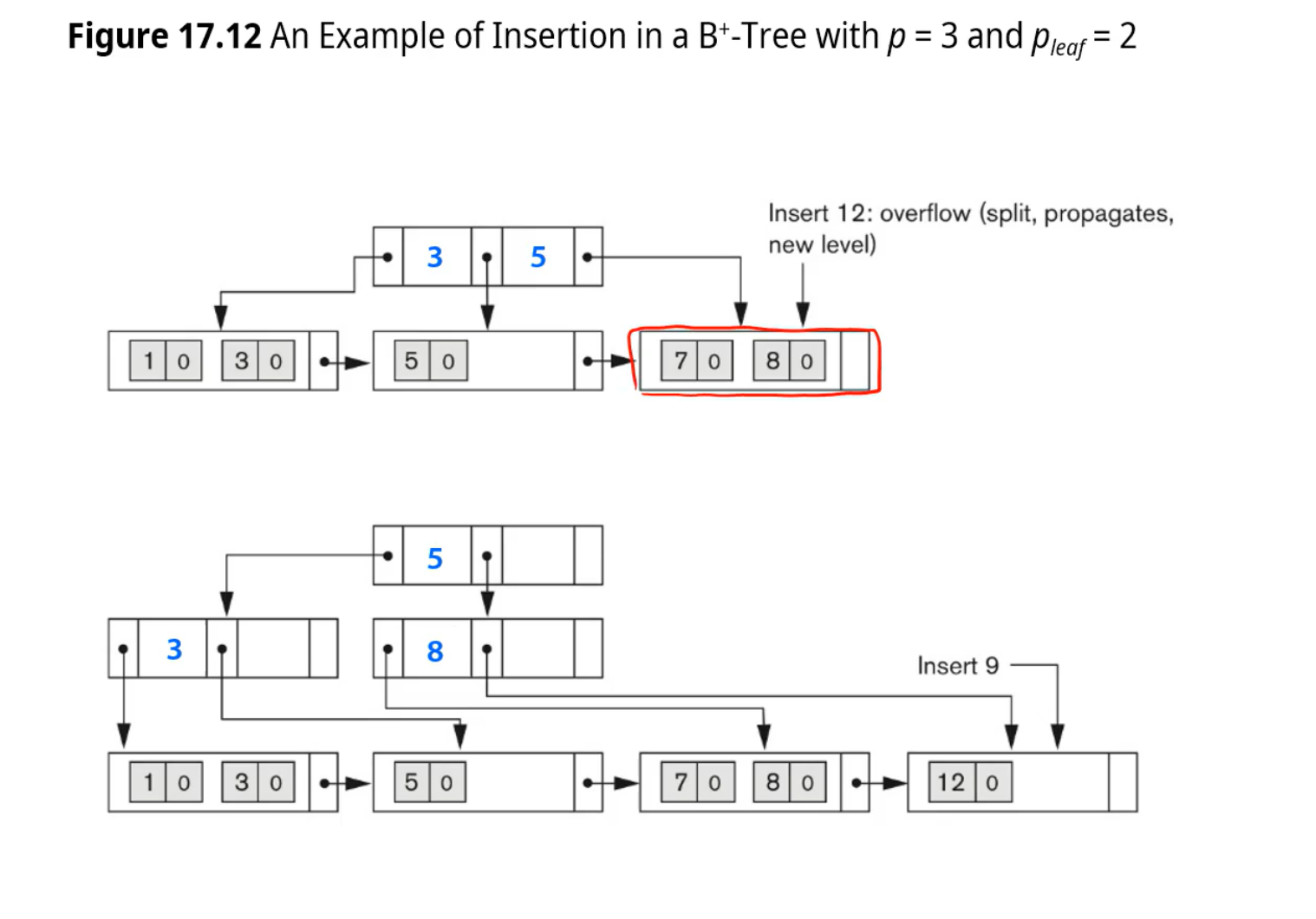
internal node : Btree와 같이처리
Leaf node : 키값을 상위 노드에 남겨놔야 한다 => 헷갈리면 안되여
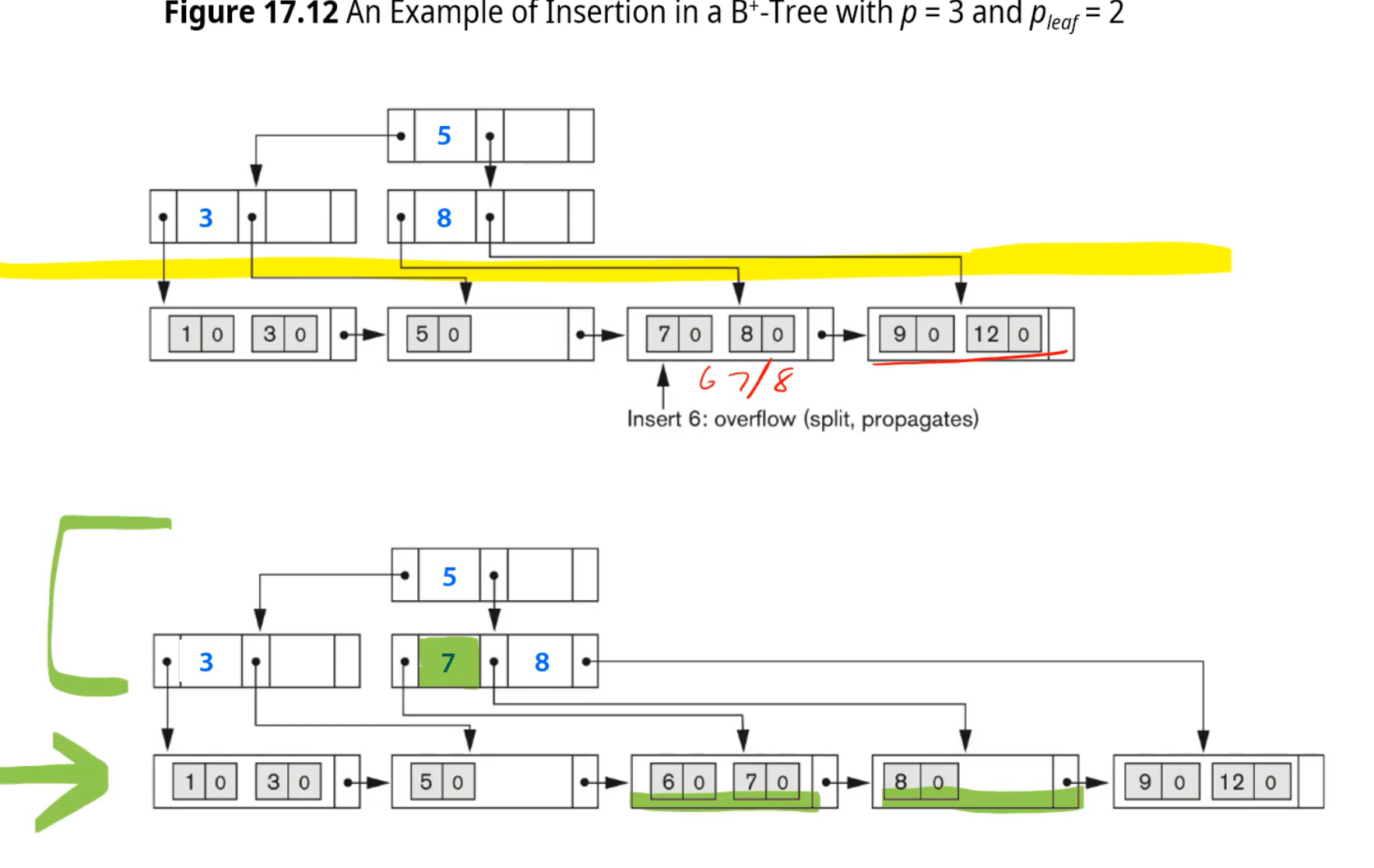
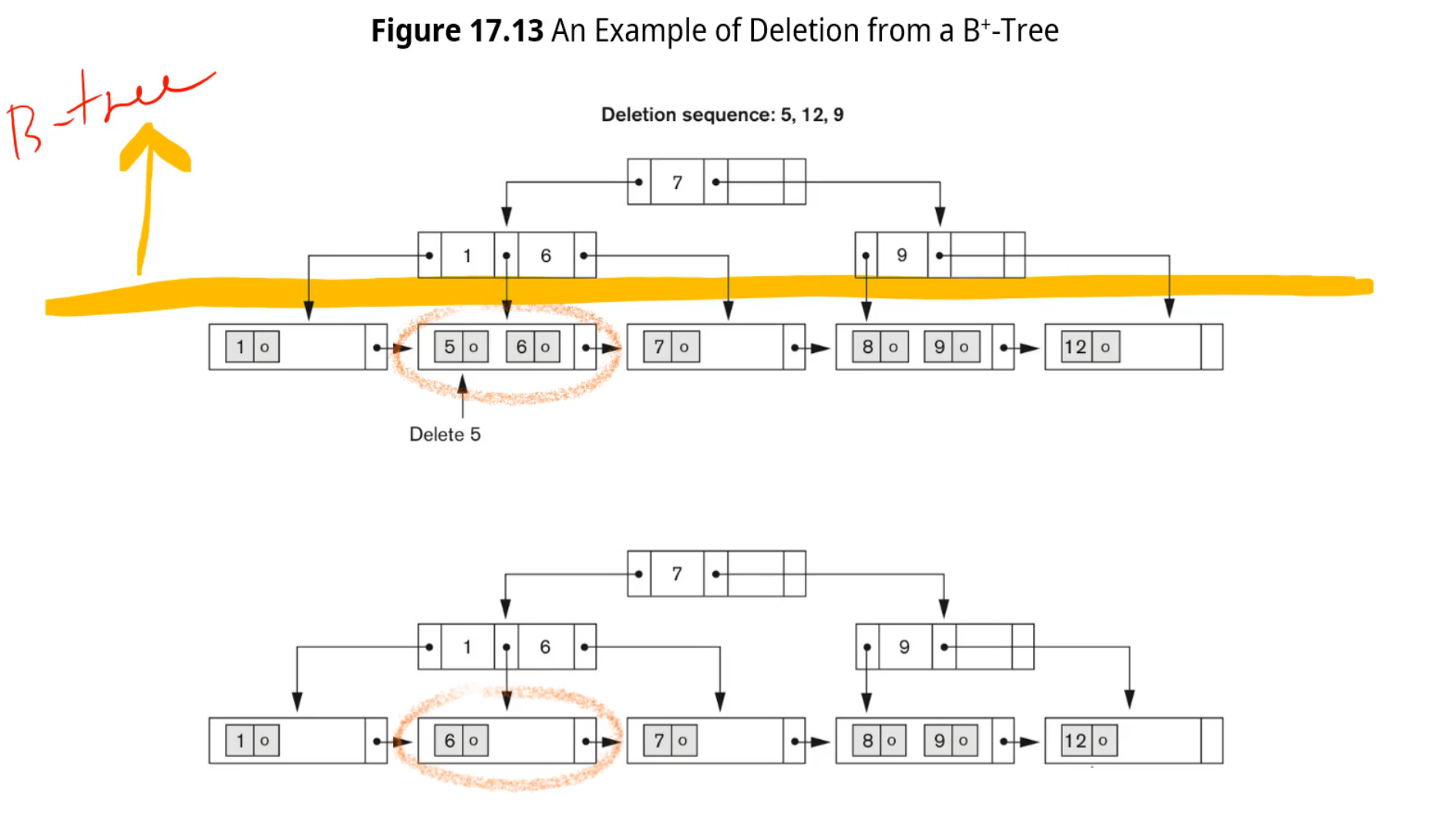


마지막으로 8을 삭제하면, 루트는 1,6 리프에는 1,6,7이 존재하는 B+tree가 생성된다
이러한 모든 index는 유저 마음대로 생성하며, 사용은 dbms가 알아서 처리한다
'Database' 카테고리의 다른 글
| Database 21,22장 (0) | 2020.12.02 |
|---|---|
| Database 20장 (0) | 2020.12.01 |
| Database-16 (0) | 2020.11.05 |
| Database-16장 (0) | 2020.10.22 |
| Database - 10장 (0) | 2020.10.22 |



